Дискуссии - Наука

С.Л. Василенко

Аннотация. Конструктивная критика – руководство-наставление избегать ошибки в будущем. Она направлена не столько на персону, сколько на читательскую аудиторию. Главное прислушаться, оценить и на свежую голову спокойно осмыслить. Дальше дело техники. Что-то отметается, часть принимается, направляясь на совершенствование и развитие. Непроторенной дорогой к новым знаниям.

«Глокая куздра штеко будланула бокра и курдячит бокрёнка», Л.Щерба, 1928.

Вступление. Знаменитая фраза академика Л.Щербы не имеет смысла. Но прекрасно демонстрирует узнаваемость частей речи (существительного, прилагательного, глагола, наречия) по их характерным признакам – окончаниям и суффиксам.

Этим грамматика похожа на геометрию, воплощая стройность, четкость и определенный порядок, в котором элементы выполняют собственные функции, а в интегральном виде – генерализацию, обобщение и целостность.

«Геометрия не говорит об этом вот кубике или о тех двух треугольниках. Она устанавливает свои законы для всех вообще кубов, шаров, линий, углов, многоугольников, кругов, какие только могут найтись на свете», – Л.Успенский (Слово о словах, 1962).

"Мета-геометрия" (P.Mansion, Metageometrie, 1896) и/или метагеометрическая философия (М.Аксенов, 1896) своим формообразованием созвучна метафизике [1] и по определению должна охватывать наиболее общие закономерности, быть свободной от метрики – инварианта расстояния и, как строго отвлеченная геометрия <миропорядка>, становиться фундаментом-первоосновой для других геометрий. Подобно проективной геометрии, которая практически свободна от инвариантов и более остальных вплотную приблизилась к пониманию сущности приставки "мета" (греч. meta вслед за, после, сверх).

Единственный инвариант проективной геометрии – это сложное отношение четырех точек на прямой линии. Плюс особая единичная точка нормирования. Выдающийся английский геометр А.Кэли показал, что геометрии Евклида, Лобачевского, Римана, Минковского, аффинные и другие геометрии – частные случаи проективной геометрии, в которой сфера с отождествленными диаметрально противоположными точками – суть проективной плоскости. Окружности и сферы, тетраэдры и додекаэдры становятся лишь различными видоизменениями и частными случаями общих идей проективной геометрии.

Британский математик Ч.Хинтон называл метагеометрией систему исследования "высшего пространства" с четвертым измерением (1904), хотя неправомерно связывал её с неевклидовой геометрией, которая по размерности пространства стоит к метагеометрии в таком же отношении, как эвклидова геометрия [2, гл. 7].

Создание "мета-геометрии" пока остается открытой проблемой, где та или иная геометрия играет роль системы координат, а законы и соотношения формулируются на некотором метагеометрическом (надгеометрическом) языке, который инвариантен относительно смены геометрий и не зависит от конкретного вида меры. Как комплексная "обобщающая теория геометрических теорий", которая объемлет любые отношения и формы, возникающие при рассмотрении однородных объектов, явлений и событий вне их конкретного содержания, и сходные с обычными пространственными отношениями и формами. Теория, в которой линии не обязательно "привязаны" и/или представимы на геометрических поверхностях.

Тем очевиднее становится глубокое неустранимое противоречие между формой и содержанием "мета-геометрии" одного из авторов Академии Тринитаризма (АТ), далее по тексту – писателя. С одной стороны, конкатенация высокопарных утверждений типа «впервые решены фундаментальные задачи», гиперболизация результатов, непременное подчеркивание содержание некоего «нового научного знания в области числа и геометрии». С другой стороны, необоснованность утверждений, калейдоскоп неточностей, противоречий, простых, но утомительных выкладок-представлений на фоне отсутствия точной геометрии как таковой. Причем, под маской некоего национального русского проекта, когда любая критика персонифицируется с наклеиванием ярлыков: ах, вы не согласны с моим мета-абстрагированием, значит, русофобы. Видимо, невдомек, что вектор развития геометрии разворачивает к плинтусу он сам.

Писательская "мета-геометрия" с её рассогласованностью, мифами и ошибками уже рассматривалась с разных ракурсов в наших статьях: Золотоносная атрофия, Доверяй, но проверяй (4 заметки), Треугольник Кеплера как объединитель теоремы Пифагора, золотого сечения и современных мифов, О преемственности и единении знаний в золотоносной тематике, Золотой прямоугольник Кеплера, Фибоначчиевый ряд золотых треугольников Кеплера и др. Повторяться не будем.

Отметим лишь некоторые новые проявления неудержимого полета писательско-творческой фантазии. Не столько для него, сколько для заинтересованного читателя.

Выборочные апокрифы к геометрии.

1) Писатель считает, что «Фундаментальным основанием метрики математики Евклида является десятеричная система исчисления» (АТ, 04.05.2016). – Аксиомы Евклида описывают метрические свойства пространства: однородность, изотропность, непрерывность. В его "Началах" используется также понятие общей меры чисел, например: «Для двух данных чисел, не первых между собой, найти общую их меру» (Предложение 3, книга 7). Однако в доказательных описаниях нет ни самих чисел, ни малейших признаков на десятичную систему исчисления. Есть только геометрические отрезки, которые обозначаются заглавными латинскими буквами и не связаны ни с какой системой счисления. Напомним также, что слова "исчисление" calculus и "счисление" numeral в математике обозначают разные понятия.

2) Писатель никак не разберется с мерой длины и в зависимости от ситуативного настроя буквально мечется между "умной" единичной мерой 1 и "красивой" золотоносной мерой Ф. То у него «в метагеометрии единой мерой вычислений параметров всех геометрических фигур является произвольный раствор циркуля r = 1» (АТ, 07.02.2018). То буквально через 40 дней: «в метагеометрии единой мерой длины является не "1", а число Ф = 1,618…» (АТ, 18.03.2018).

Между тем, со слов писателя, фундаментальные задачи (построение пятиугольной пирамиды с 12 ребрами, предвидение скорости потепления климата, решение четвертой проблемы Гильберта и др.) он решил на основе сакрального мета-треугольника (a, b, c) = (√Ф, Ф, Ф√Ф) с высотой h = 1. Поэтому мерой может выступать как 1, так и число Ф ≈ 1,616.

При этом остаются открытыми два вопроса: а) какова система счисления для самого числа Ф; б) если Ф – мера длины, то все вычисления должны быть привязаны исключительно к нему как в системе счисления Бергмана, подробно описанной проф. А.Стаховым – представителем славянской группы "золотосеченцев", от которой писатель демонстративно отмежевался. Иначе излюбленная писательская запись типа «сторона ромба равна 2,0581710272714922503219810475804…» теряет смысл.

«Наши доказательства не могут совпадать потому, что одни и те же геометрические объекты измеряются разными мерами». – Утверждения в геометрии доказываются логическим путем, поэтому выбор конкретной меры (1 или Ф) на них не влияет.

3) Для развития некоего русского проекта некоей математики гармонии, писателю «потребовалось переосмысление проблемных НАЧАЛ Евклида в области геометрического построения и вычисления гармоничных отношений» (АТ, 29.01.2021). – Это о чём? Каких таких проблем и проблемных начал, в каких предложениях Евклида? О гармонии в евклидовой геометрии тоже нет ни слова. Никаких упоминаний, кроме математических пропорций, что не одно и то же.

4) Писателю «всё явственней становилось назидание Пифагора о том, что, если возникла проблема, ищите треугольник и она будет уже на треть решена». – Откуда это? Где и когда озвучено такое назидание? Французы в подобных случаях говорят: ищите женщину. Или Пифагор имел в виду любовный треугольник, о чём история умалчивает. Она не оставила свидетельств и об упомянутом назидании. Разве что в оккультной книге М.Холл отмечал, как во имя общей мудрости Пифагор учил представлять каждую проблему в виде треугольной диаграммы: «Узрите треугольник, и проблема на две трети решена… Все вещи состоят из трех» [3, с. 226].

Всё-таки одна треть и две трети ощутимая разница. Да и речь шла об особом треугольнике – равносторонней фигуре с направленной вверх вершиной, символе полноты гармонии, как и в Древнем Египте, где основание обозначает устойчивость. Стороны делились на три равные части, в центре ставилась точка, образуя священно-божественную тетрактиду (четверицу) 1 + 2 + 3 + 4 = 10, которая в глазах пифагорейцев означала совершенство, гармонию и воплощала природу Вселенной.

5) Утверждение писателя «… в эллипс нельзя вписать квадрат» (АТ, 04.05.2016) является неверным. Отсутствие в литературе соответствующих построений ещё ни о чём не говорит. Из канонического уравнения эллипса x²/a² + y²/b² = 1 с полуосями a, b следует, что половина стороны вписанного квадрата равна ab/√(a² + b²).

Половина площади прямоугольного треугольника с катетами a, b равна ab = ch, где h – высота, проведенная из вершины прямого угла на гипотенузу c.

Откуда следует h = ab/c = ab/√(a² + b²).

Таким образом, сторона вписанного квадрата равна удвоенной высоте прямоугольного треугольника, построенного на полуосях эллипса.

Алгоритм вписывания несложный (см. рисунок): вычерчивается эллипс, на его полуосях достраивается прямоугольный треугольник, в нём проводится высота h, которая восстанавливается на вертикальную полуось, и через полученную точку достраивается собственно квадрат.

6) Одну статью (АТ, 02.07.2014) писатель начинает тремя цитатами Пушкина, Пифагора, Кеплера и рядом с ними приводит эпиграф имени себя: «Треугольник, у которого произведение не равных катетов численно равно гипотенузе, есть третье сокровище геометрии». – Напыщенность слога нарочито превознесена, но чем обусловлена, не понятно. В прямоугольном треугольнике произведение катетов a·b численно равно произведению гипотенузы c на высоту h, опущенную из прямого угла. То есть a·b = c·h, по определению. Достаточно положить h = 1 и получить a·b = c. Где и какая здесь жемчужина-изюминка? Информационная новизна стремится к нулю. Или приравнять c = 1, тогда a·b = h, и так далее. Всё элементарно. Без клада сокровищ.

Проводятся две горизонтальные линии с зазором 1 и между ними чертятся любые прямоугольные треугольники, образуя "танцующие" в обе стороны катеты: один приближается к вертикали, другой удаляется от неё, вплоть до бесконечности.

Катеты взаимосвязаны формулой a² = 1/(1 – b^–2), сумма углов их наклона равна 90⁰.

7) «Додекаэдр является пределом развития правильных многогранников Платона, поскольку только двадцать точек-вершин равномерно распределяются на сфере и сходятся в одной точке в центре сферы» (АТ, 07.02.2018). – Почему только и именно 20? Каким образом они могут сходиться в центре сферы? Если на сфере можно равномерно распределить сколь угодно точек по заданному критерию.

Факт наличия в трехмерном пространстве только пяти правильных выпуклых многогранников хорошо известен, но он следует совершенно из других соображений.

«Их часто называют платоновыми телами, так как они играют большую роль в натурфилософии Платона» [4, с. 100]. Первое известное доказательство того, что их ровно пять, дал ещё древнегреческий математик Теэтет Афинский (около 417–369 год до н. э). Он же открыл икосаэдр и додекаэдр.

Пусть пара целых чисел {p, q} характеризует односвязное платоново тело, в котором к каждой вершине примыкают q граней в виде правильных р-угольников с внутренними углами 180·(1–2/р) градусов. Из выпуклости многогранника следует, что сумма всех внутренних углов по граням, примыкающим к любой из его вершин, меньше 360⁰. Следовательно, должно выполняться неравенство 180·(1–2/р)q < 360, которое равносильно q(р–2) < 2p или p(q–2) < 2q. Отсюда вытекает, что p, q > 2, а возможные решения определяются простым перебором многогранников {p, q}: p = 3, q = 3, 4, 5, {3, 3}, {3, 4}, {3, 5}; p = 4, q = 3, {4, 3}; p = 5, q = 3, {5, 3}; p > 5 – решений нет.

8) Писатель носит мета-Δ как писаную торбу. На практике всё сводится к простому умножению "золотого тождества" 1 + Ф = Ф² на константу Ф и последующему его представлению по теореме Пифагора: (√Ф)² + Ф² = (Ф√Ф)². Собственно и весь мета-Δ", как частный случай Δ-Кеплера. Без дополнительных общих фраз о сакральной геометрии, трансцендентности и прочего искусственного "обнаучивания" данного числового тождества. В таком же виде можно представить и другие числовые тождества с золотой константой Ф = ф^–1: 1² + (√Ф)² = Ф², ф² + (√ф)² = 1,...

Многогранники Джонсона. Писатель утверждает, что им «впервые (?) построена правильная 5-гранная пирамида, у которой все боковые грани – равносторонние треугольники». – Грустно от таких слов. Что здесь такого геометрически особенного, чтобы переключать внимание на первооткрывателя имени себя? Или она доселе не изучена? Пятигранная пирамида, это какая? Четыре боковых грани плюс грань-основание или пять боковых граней, которая называется пятиугольной? – В любом случае развертку правильной пирамиды строят обычные школьники, исходя из её определения.

Но писатель превозносит это до небесных высот вавилонской башни как "решение фундаментальной (?) задачи": «построена геометрическая модель пространства правильной 5-угольной пирамиды, у которой все 12 ребер равны... Жреческие мистерии, например, их представитель Платон, не знали моделей "сакрального прямоугольного тетраэдра" и правильной 5-угольной пирамиды, у которой все 12 ребер равны. Если бы они имели знание об этих моделях, то при фараоне Хеопсе, думается, был бы заложен фундамент правильной 5-гранной пирамиды» (АТ, 29.01.2021). – И хорошо, что не знали такой экзотической пятиугольной пирамиды, ибо пятиугольная пирамида имеет 10, а не 12 ребер: пять в основании и пять боковых. Двенадцать ребер имеет гипотетическая вырожденная 6-угольная пирамида, которая складывается на плоскости в правильный шестиугольник со всеми диагоналями, а также удлиненная треугольная пирамида Джонса J₇ с семью правильными гранями (4 треугольника и 3 квадрата), которая образуется соединением тетраэдра и правильной треугольной призмы.

Касательно "впервые", "фундаментальности" и подобной высокопарности напомним про тела Джонсона (Johnson Solid) – выпуклые с правильными гранями неоднородные многогранники, отличные от призм, антипризм, правильных (платоновых) и полуправильных (архимедовых) многогранников. Норман Джонсон первым перечислил и описал (1966) такие 92 многогранники [5], получаемые смешением различных правильных многоугольников. Русифицированные названия приведены В.Залгаллером [6, с. 20-24]. Он же доказал (1966) полноту классификации Джонса, поблагодарив за помощь ленинградских 10-классников и дожив в Израиле до 99 лет.

Одним из тел является пятиугольная пирамида, ограниченная пятью боковыми равносторонними треугольниками и одним пятиугольником в основании: всего 6 граней, 10 ребер и 6 вершин. Это второй многогранник J₂ в списке Джонсона.

Легко показать, что пятиугольная пирамида J₂ с длиной ребра 1 имеет высоту h = √(2−ф)/√5 ≈ 0,5257 – очень мелкая пирамида, больше похожая на шляпку-шестиуголку. Такие пирамидки никак не могут заполнить додекаэдр, разве что немного прикрыть его реберный каркас, как крышка сковороду. Зато могут присоединяться к нему снаружи, образуя разные вариации увеличенного додекаэдра J₅₈ – J₆₁.

Две пятиугольные пирамиды при соединении оснований образуют 5-угольную бипирамиду J₁₃, которая важна в проблеме Томсона с электронами. Причем весьма оригинально: точное решение дал компьютер (2010), а математикам не под силу. Действительно, фундаментальная задачка и дело чести теоретической мысли. Хотя бы потому, что могла бы приблизить к разгадке феномена живого вещества с его характерными признаками осевой симметрии пятого порядка.

Неидеальная идеальность додекаэдра. Тетраэдр, октаэдр, икосаэдр образуются треугольниками, додекаэдр – пятиугольниками, в которых не оказалось места треугольникам Платона. Первые три тела и куб в трактате "Тимей" он связывал с четырьмя базовыми стихиями-элементами: земля, огонь, воздух, вода. Стихии закончились, совершенная тетрактида исчерпалась, и про додекаэдр философ лишь невнятно заметил: «В запасе оставалось еще пятое многогранное построение: его бог определил для Вселенной и прибегнул к нему, когда разрисовывал её и украшал» [7, гл. 17]. – Такая себе игра фантазии ученого с картинками-раскрасками и елочными висюльками. Что в голову взбрело. Так же как «никакого тяготения на расстоянии быть не может», «человек имеет две души» и многое другое…

В математике известна проблема равномерного распределения (оптимальной упаковки) n точек на сфере [8], которая входит в число 18 ключевых задач С.Смейла.

Существует ряд одинаково состоятельных критериев для описания степени равномерности распределения точек на сфере, примерно или строго равноудаленных друг от друга. Наиболее распространенный из них составляет открытую математическую проблему минимакса: разместить на сфере n точек так, чтобы наименьшее из парных расстояний между ними было максимальным.

Известна также похожая проблема Томсона (1904): определить минимальную конфигурацию полной потенциальной энергии электростатического заряда для n электронов, которые отталкиваются друг от друга согласно закону Кулона, а своим местонахождением ограниченны поверхностью единичной сферы.

Примерные решения (за исключением случаев n = 4, 6, 12, 24 выпуклая оболочка только топологически эквивалентна многограннику):

n = 2 – двуугольник digon;

n = 3 – равносторонний треугольник triangle на большой окружности;

n = 4 – тетраэдр tetrahedron;

n = 5 – треугольная бипирамида triangular bipyramid J₁₂, составленная из двух тетраэдров, как математически строгое компьютерное решение (2010);

n = 6 – октаэдр octahedron;

n = 7 – пятиугольная бипирамида pentagonal bipyramid J₁₂; наилучшим решением на сфере являются четыре равносторонних сферических треугольника с углами 80 градусов;

n = 8 – квадратная антипризма (антикуб, витой куб) square antiprism. Антипризма – полуправильный многогранник, у которого две одинаковые параллельные грани-основания – правильные m-угольники, а остальные 2m боковые грани – правильные треугольники;

n = 9 – трижды наращенная треугольная призма triaugmented triangular prism J₅₁; наилучшее решение на сфере – восемь равносторонних сферических треугольника с углами arccos(1/4);

n = 10 – скручено-удлиненная четырехугольная бипирамида gyroelongated square bipyramid J₁₇;

n = 12 – икосаэдр icosahedron;

n = 20 – компьютерное решение, без четкой ассоциации на известный многогранник;

n = 24 – регулярный курносый (плосконосый) куб snub cube, полуправильный многогранник (архимедово тело). Имеет 38 граней (32 треугольника, 6 квадратов), 60 ребер одинаковой длины, 24 вершины. Является хиральным (без зеркальной симметрии). Метрические свойства определяются константой трибоначчи – действительным корнем t кубического уравнения x³ = x² + x + 1. В декартовой системе координаты его вершин определяются перестановкой троек чисел (±t, ±1, ±t^–1). Название "курносый куб" cubus simus дал И.Кеплер в трактате Harmonices Mundi, 1619;

n = 32 = 2⁵ – полуправильный многогранник (каталонское тело, двойственное усеченному икосаэдру – архимедову телу), созданный путем присоединения пятиугольной пирамиды к каждой грани додекаэдра. Его 60 граней – равнобедренные треугольники с углом при основании arcos[(5 – Ф)/6] ≈ 55,69⁰.

12 точек, заданных циклическими перестановками координат (0, ±1, ±Ф), являются вершинами правильного икосаэдра. Его двойственный додекаэдр, ребра которого пересекаются с ребрами икосаэдра под прямым углом, в качестве вершин имеет точки (±1, ±1, ±1) вместе с точками (±Ф, ±ф, 0) и циклическими перестановками этих координат. Умножение всех координат икосаэдра на коэффициент (3Ф+12)/19 ≈ 0,887 дает немного меньший икосаэдр. Его 12 вершин вместе с вершинами додекаэдра являются вершинами пентакисдодекаэдра с центром в начале координат. Длина его длинных ребер равна 2ф. Отношение длин сторон треугольников равно (5 – Ф)/3 ≈ 1,127.

Вопреки ожиданиям, два платоновых тела – куб (n = 8) и додекаэдр (n = 20) не являются оптимальными конфигурациями в задаче Томпсона. Так же как и плосконосый двуклиноид или сиамский додекаэдр J₈₄, имеющий 12 граней – правильных треугольников и n = 8 вершин.

Додекаэдр обладает осью симметрии 5-го порядка, которая не совместима с трансляционной инвариантностью. Поэтому никакой идеальный кристалл не может обладать такой симметрией.

Возникает своеобразный парадокс. Додекаэдры физически не реализуются, ими нельзя заполнить евклидово пространство, но дают самую плотную конусную упаковку евклидового пространства ρ = 6·(1 – sin arctg Ф)·100 ≈ 89,6 % [9].

Конусность проявляется в практической и теоретической физике: эффект Черенкова, световой конус в теории пространства-времени, временные сечения таких конусов в виде окружностей, лежащих в ортогональной плоскости, и др.

Звездчатые тела. Писатель отмечает: «К основным пяти Платоновым телам относятся: октаэдр, звездный тетраэдр...» (АТ, 07.02,10.03.2018).

Нет основных или неосновных (дополнительных) платоновых тел, их всего пять! Звездных тел также не бывает. Разве что красивые формы знаменитостей – селебрити.

В геометрии есть звездчатые многогранники – невыпуклые тела с пересекающимися гранями, которые не относятся к платоновым телам, по определению. Грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются ребрами. Звездчатая форма многогранника получается путем продления его граней через ребра до их следующего пересечения с другими гранями по новым ребрам.

Тетраэдр и куб не имеют звездчатых форм, поскольку их грани при продлении через ребра более не пересекаются. Октаэдр имеет только одну звездчатую форму (её открыл Кеплер и назвал Stella octangula – звезда восьмиугольная, как соединение двух тетраэдров), додекаэдр – 3, икосаэдр – 59.

Циркуль и линейка. «Построения с помощью циркуля и линейки без делений, а также вычисления параметров 5-гранной пирамиды, боковые грани которой – равносторонние треугольники, в классической геометрии Евклида мы не находим. Почему? Думается, этим вопросом задавались многие творцы и исследователи математики. Ответ на него в математике остается "белым пятном"» (АТ, 07.02,10.03.2018). – Не находим, поскольку построения с помощью циркуля и линейки без делений относятся к плоским фигурам, но не к телам! В задачах на построение рассматривается множество точек, прямых линий и окружностей плоскости. Никаких тел! Тем, более «геометрического построения додекаэдра с помощью циркуля и линейки без делений». Разве что разверток поверхностей (всех граней).

То есть можно построить развертку пятиугольной (!) пирамиды. Но здесь всё элементарно. Достаточно из вершин правильного пятиугольника провести пересекающиеся засечки радиусом, равным стороне. Ни белых пятен вам, ни вопросов.

Боковые грани правильной равнобедренной n-угольной пирамиды – равносторонние треугольники, поэтому все плоские углы n-гранного угла при вершине пирамиды равны 60⁰. Сумма плоских углов выпуклого многогранного угла 60⁰n < 360⁰ или n < 6. Значит, есть только три пирамиды: 3-угольная (правильный тетраэдр), 4-угольная и 5-угольная.

Прямоугольные треугольники Кеплера и Фибоначчи. На евклидовой плоскости тупых и острых углов множество. Прямой угол – один единственный, и в пределах своего вида он не может быть больше или меньше. «Это "золотая середина" (aurea mediocrita) между избытком и недостатком, если воспользоваться выражением, которое употребил Гораций в оде II.3» [10].

Плоский треугольник имеет три степени свободы и задается тремя параметрами (сторонами и углами), из которых хотя бы один метрический.

Прямой угол снимает степень свободы, давая взамен теорему Пифагора c² = a² + b².

1) Введем ещё одно дополнительное условие: геометрическая прогрессия величин сторон c/b = b/a или b² = ac, то есть c² = a² + ac.

Разделив равенство на ac, и обозначив x = c/a, получаем уравнение x² = x +1 с действительным корнем x = Ф = (√5 + 1)/2 – константой золотой пропорции.

Треугольник Кеплера – это прямоугольный треугольник, длины сторон которого составляют геометрическую прогрессию (a : b : c) = (1 : √Ф : Ф) или в эквивалентном виде (ф : √ф : 1), где ф = Ф^–1 = (√5 – 1)/2. Высоты и синусы углов тоже [11, 12].

Знаменатель прогрессии √Ф – для упорядоченной тройки сторон по возрастанию или √ф – по убыванию. Логарифмы сторон образуют арифметическую прогрессию.

Впервые такой треугольник описал Кеплер в письме своему учителю [13, с. 149].

Пропорциональность сторон вкупе с прямоугольностью приводит к тому, что знаменатель геометрической прогрессии для численных значений сторон равен квадратному корню из константы золотого сечения Ф ≈ 1,618 [14, с. 80–90].

Треугольник Кеплера выступает как объединитель теоремы Пифагора и золотой пропорции [11]: геометрическая прогрессия сторон со знаменателем √Ф и площадей треугольников, разделенных высотой, со знаменателем Ф.

Высота h, опущенная из прямого угла, делит гипотенузу золотым сечением, биссектриса – на два отрезка в соотношении 1:√Ф.

Геометрическая пропорция (см. рисунок): c/b = b/a = a/h = h/c_a = √Ф.

Возрастающая геометрическая прогрессия (c_a, h, a = c_b, b, c) со знаменателем = √Ф, где каждая подряд тройка – стороны подобных треугольников: (c_a, h, a), (h, c_b, b), (a, b, c).

Δ-Кеплера – самый крупный "золотой слиток": в нём больше золотоносных пропорциональных отношений, нежели в любом треугольнике пентаграммы.

2) Если задать другое дополнительное условие: отношение катетов b/a = Ф, то получаем a²(1 + Ф²) = c² или c/a = √(1 + Ф²).

Белорусский ученый А.Ворон [15, 16] показал, что в поперечном сечении икосаэдра /додекаэдра/, проходящем через его центр симметрии и четыре противоположных вершины или два ребра, образуется шесть /четыре/ пар треугольников Кеплера (c/a = Ф) и Фибоначчи (b/a = Ф). Он же предложил последнее название. Почему бы и нет.

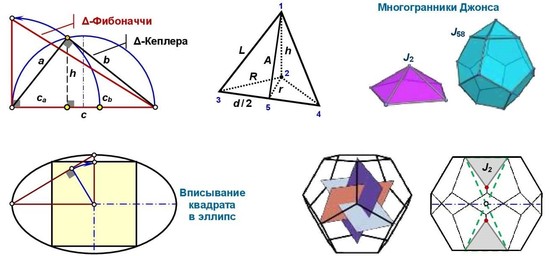
Оба треугольника принадлежат семейству золотых прямоугольных фигур [17] и чертятся просто (см. рисунок). На фиксированном отрезке строится полуокружность и точка золотого сечения любым способом. Через точку ЗС проводится дуга. Её пересечение с полуокружностью дает вершину Δ-Кеплера, с перпендикуляром – вершину Δ-Фибоначчи (прямоугольного треугольника с соотношением катетов 1:Ф).

Заметим, что две гиперболы x² – y² = 1 и xy = 1 пересекаются в точках ±(√Ф, √ф).

Корень √Ф = 1.2720196495… с точностью до 8 знаков близок к константе C = 1,2720196331… [18, А219177], которая примечательна тем, что ближайшие целые к C^t, t = 2ⁿ – простые числа, образующие ряд [18, A059785]: 2, 3, 7, 47, 2207, 4870843, 23725111530599, 562880917139361624513298747,…

Не мытьем так катанием. Приняв наши замечания-поправки [19], что "мета-Δ" с его фиксированными сторонами не вписывается в правильный додекаэдр, писатель печатает вторую версию "метагеомерии" (АТ, 10.03.2018), где выполняет странные манипуляции-преобразования: «При сжатии эллипсоидной сферы в сферу шара происходит численное преобразование параметров метатреугольника … в параметры прямоугольного треугольника».

Прежде всего, в геометрии нет понятий эллипсоидной сферы и сферы шара. Типа треугольного и/или трехстороннего треугольника.

Есть эллипсоид вращения (сфероид – по Архимеду) – поверхность вращения в 3-мерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей. Есть эллипсоид – поверхность в 3-мерном пространстве, полученная деформацией сферы вдоль трех взаимно перпендикулярных осей.

Сфера – геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы) [20, с. 54]. Сфера – поверхностью шара.

Эллипсоид с полуосями √Ф и Ф писатель масштабирует в другой эллипсоид, полуоси которого соотносятся как 1:Ф (треугольник Фибоначчи), при этом называя его сферой (?).

О нашей работе [19] ни слова, ни ссылки. А ведь именно там писателю было показано в три строчки «решение упущенной возможности»: радиус описанной окружности пятиугольника относится к высоте пирамиды, как R/h = Ф.

Но главное в другом. "Мета-Δ" оказался ненужным, поскольку не встраивается в пирамиду Джонса J₂, и меняется на золотой треугольник с соотношением катетов 1:Ф – Δ-Фибоначчи (в терминологии Ворона). Далее опять, к сожалению, как в детской поговорке: «на дворе стоит забор, а на нём мочало, наша песня хороша, начинай сначала». Всё та же навязчивая идея вмонтировать в додекаэдр пятиугольную пирамиду с правильными треугольными боковыми гранями. И снова с ошибками.

Первый раз площадь треугольного основания (см. рисунок) он определял по формуле S₁ = r/2, второй раз S₂ = r·R/2. Хотя на самом деле S = r·d/2. Отсюда и неправильные вычисления объема додекаэдра V₁ = 12,1 и V₂ = 63,9 вместо 31,5 и 75,1.

Но даже эти "подправленные значения" не дают объем додекаэдра.

Пятиугольные пирамиды Джонса J₂, которые писатель так жаждет внедрить в тело додекаэдра, невысокие и только прикрывают додекаэдр, как шапочки, образуя внутри тела большие пустоты. Одним словом, симукляр.

Параметры пирамиды Джонса J₂ с ребрами L_J2 = d: радиус описанной окружности основания-пятиугольника R = 1/(2·sin π/5)·d ≈ 0,851·d; высота h_J2 = R·ф·d ≈ 0,526·d.

Объем пирамиды Джонса J₂ определяется простой формулой V_J2 = (2 + Ф)/12·d³.

Двенадцать таких пирамид заполнят объем пространства (2 + Ф)·d³ ≈ 3,618·d³.

На самом деле боковое ребро пирамиды (радиус описанной сферы додекаэдра) должно быть L_д = Ф·√3/2 ≈ 1,401·d, высота пирамиды (радиус вписанной сферы додекаэдра) – h_д = Ф²/(4·sin π/5)·d ≈ 1,114·d,

Несовпадение очевидно, и здесь тщетны взывания писателя к «потомкам, <которым> еще предстоит оценить достоинства его доказательства» (АТ, 10.03.2018).

Для полного заполнения додекаэдра двенадцатью пятиугольными пирамидами отношение L_д/d = Ф·√3/2 ≈ 1,401 – численное значение высоты равностороннего треугольника со стороной Ф. То есть это отношение – иррациональное число, независимо от меры d. На это указывал ещё Евклид 2300 лет назад: «Составить додекаэдр, охватить его сферой... и показать, что сторона додекаэдра будет иррациональной – так называемым вычетом» [21, с. 132]. И никакой навязчиво-надоедливой обсессии писателя о внедрении в додекаэдр пирамиды Джонса J₂ с равенством всех её ребер L = d.

Любая "триалектика" здесь также, увы, бессильна. В какую бы национальную символику самоидентификации её не облачали. Достаточно вычертить развертку, склеить 12 пирамид и собрать из них додекаэдр. Без лишних упований на метагеометрию.

Единственным критерием истины является опыт (Леонардо да Винчи). – Прочее малополезно и бесперспективно...

Да и зачем вообще "городить огород", если давно известно, что объем додекаэдра равен V = d³·(15+7√5)/4 = 5/2·(dФ)³ / (2 – ф), где d – длина ребра.

Не множьте сущее сверх необходимого... (Оккама, 14 век).

Нет нужды искать золотые прямоугольные треугольники с отношением сторон 1:Ф там, где их нет. Лучше констатировать их реальное присутствие. Например, соединение центров граней додекаэдра дает три взаимно перпендикулярных золотых прямоугольника [22, с. 57-58], составленных из двух золотых треугольников.

В изобразительном искусстве и математике известна обширная коллекция невозможных объектов – особого вида визуальной иллюзии, таких как бесконечная лестница Пенроуза (1958) – лауреата Нобелевской премии по физике (2020), треугольник Рутерсварда (1934), куб Эшера (1958) и многие другие. Теперь к ним можно присовокупить на равных правах и невозможный додекаэдр Сергиенко.

Додекаэдрическое пространство Пуанкаре. Писательские работы (АТ, 10–18.03.2018) как кружева сотканы из набора фрагментов Интернета без единой ссылки, отвечая в этом контексте их эпиграфу: «Всё гениальное просто, а простое гениально». «Моё исправленное доказательство гипотезы Пуанкаре о "додекаэдровой Вселенной" (АТ, 10.03.2018) сводится к тому, что додекаэдр, вписанный в шаровую сферу, состоит из 12 пятигранных пирамид, грани которых являются равносторонними треугольниками… В метагеометрии грани пирамиды – равносторонние треугольники. Из таких пирамид структурно без пустотных зазоров состоит додекаэдр Платона-Пуанкаре» (АТ, 18.03.2018). – Выглядит наивно и даже комично. Такой гипотезы никогда не было. Гипотеза Пуанкаре (1904) – всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере – доказана Г.Перельманом.

Додекаэдрическое пространство Пуанкаре (гомологическая сфера Пуанкаре) – замкнутое сферическое 3-многообразие, геометрическая модель конечного положительно искривленного пространства. Регулярный 4-мерный многогранник, как 4-мерный аналог правильного додекаэдра (додекаплекс, гипердодекаэдр), состоит из 120 ячеек-додекаэдров, с топологическим склеиванием противоположных граней додекаэдров, что в трехмерном пространстве сделать невозможно.

120 сферических додекаэдров покрывают поверхность гиперсферы – трехмерной поверхности четырехмерного пространства. Каждый сферический додекаэдр – додекаэдрический кусок гиперсферы. При построении сферического додекаэдра Пуанкаре 30 ребер додекаэдра сходятся вместе в десять групп по три ребра в каждой, в результате чего двугранные углы равны 120⁰ [23]. Что отвечает выводам Арнольда–Крылова [8].

Вычертить развертку додекаэдра Пуанкаре циркулем и линейкой, также невозможно. Да и не нужно. Подобные задачи решаются с помощью компьютерных технологий по визуализации 4-мерных тел. Псевдодоказательство гипотезы Пуанкаре в дополнительных комментариях не нуждается.

«На основе параметров пространства правильной 5-угольной пирамиды, впервые (?) ее формами геометрически заполнен пространственный континуум трехмерного объема додекаэдра». – Что здесь впервые? Из стереометрии известно, что любой выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника. Воистину впервые то, что писательские пирамидки не заполняют додекаэдр.

Арифметика и геометрия – два корня единого древа математики.

Арифметика и геометрия не только взаимосвязаны, но и служат истоками общих идей, методов и теорий. Уже простое измерение длины – есть их соединение: откладываем геометрически, считаем арифметически.

Утверждение. Арифметическая и геометрическая прогрессии совместимы только для равных величин. Согласно принципу достаточного основания (everything must have a reason or a cause – всё должно имеет резон или причинность), для доказательства логично рассмотреть только три величины a, b, c:

– арифметическая прогрессия c – b = b – a, b = (a + c)/2;

– геометрическая прогрессия c/b = b/a, b² = ac;

– объединение свойств [(a + c)/2]² = ac → (a – c)² = 0 → a = b = c.

Следовательно, приращение арифметической прогрессии = 0, знаменатель геометрической прогрессии = 1.

В частности, одновременное сочетание арифметической и геометрической прогрессии характерно для длин сторон равностороннего треугольника, и вообще для любого правильного n-угольника, включая предельное превращение в окружность, n → ∞.

Саму окружность можно рассматривать как бесконечную арифметически-геометрическую прогрессию одинаковых по модулю величин (точек) на комплексной плоскости относительно начала координат. – Своего рода единение арифметики и геометрии. Проводя циркулем окружность, мы фактически выстраиваем непрерывную последовательность точек – величин арифметико-геометрической прогрессии.

К прямоугольному треугольнику (a, b, c) = (3, 4, 5) принципиально неприменимы свойства геометрической прогрессии сторон.

Также как целое число не может быть одновременно четным и нечетным.

По улицам слона водили... Писатель приводит (АТ, 04.05.2016) некие формулировки "аксиом", например:

– «Высота треугольника, опущенная с вершины его прямого угла на гипотенузу, численно равна его площади». – Удвоенная площадь любого прямоугольного треугольника (a, b, c) равна 2S = ab = ch, по определению. Поэтому высота численно равна площади h = S только для гипотенузы c = 2.

– «Высота треугольника, опущенная с вершины его прямого угла на гипотенузу и делящую её на две части, численно равна корню квадратному из произведения её частей». Если c_a, c_b – сегменты гипотенузы, то формула h = √(c_ac_b) справедлива исключительно для треугольника Кеплера, в котором длины сторон и высота составляют геометрическую прогрессию c/b = b/a = a/h, и как следствие c_a/h = h/c_b.

Последнюю форму писатель неправомерно распространяет на египетский треугольник (a, b, c) = (3, 4, 5), "доказывая", что его «прямоугольность не соответствует истине».

Египетский треугольник имеет арифметическую, но не геометрическую прогрессию сторон, поскольку c/b = 5/4 ≠ b/a = 4/3, поэтому формула h = √(c_ac_b) к нему не применима.

Высота равна h = 3·4 / 5 = 2,4, но не как у писателя √(2·3) = √6 ≈ 2,4495…

Сегменты гипотенузы соответственно равны (c_a; c_b) = (1,8; 3,2), но не 2 и 3.

Всё остальное – "мета-геометрия" сюрреализма: «египетский треугольник (арифметический) не вписывается в окружность диаметром равным 5 единицам, не является строго прямоугольным, целочисленные (арифметические) параметры египетского треугольника несоизмеримы с геометрическими параметрами прямоугольного треугольника». – Всё как раз наоборот: египетский треугольник, свободно вписывается в окружность диаметром = 5, является строго прямоугольным, все его метрические параметры (стороны, высота, сегменты гипотенузы) соизмеримы.

Египет тоже на месте! Правда понемногу ветшает пирамида Хеопса, с которой писатель связывает основы измерительных инструментов и метрики (АТ, 10.03.2018).

Египетский треугольник (a, b, c) = (3, 4, 5) – базовая пифагорова тройка, уникальная тем, что целочисленные стороны образуют арифметическую прогрессию.

Более того, это единственная тройка с подряд идущими числами.

Действительно, (n –1)² + n ² = (n +1)², откуда следует n = 4.

Кроме того, (3, 4, 5) – единственная пифагорова тройка, содержащая квадрат, соседи которого – простые числа. Пусть b = n². Если n – нечетное, то n² ± 1 – четные, то есть не простые. Если n = 2k – четное, то (2k)² – 1 = (2k – 1)(2k + 1) – составное при любом k, кроме k = 1, то есть n = 2 и b = n² = 4.

Радиус вписанной в треугольник окружности равен единице. Более подробно его свойства, в том числе золотоносные, описаны в работе [24].

Уникальное тождество 3² + 4² = 5² дополняется другим исключительным равенством 3³ + 4³ + 5³ = 6³, то есть куб с ребром 6 равновелик сумме трех кубов с ребрами 3, 4 и 5.

Это выводит на обобщенную задачу: найти последовательности из n + 1 натуральных чисел, для которых n-я степень последнего члена последовательности равна сумме n-х степеней предыдущих членов:

n = 2: (3, 4, 5);

n = 3: (3, 4, 5; 6);

n = 4: (30, 120, 272, 315; 353);

n = 5: (19, 43, 46, 47, 67; 72};

n = 7: (127, 258, 266, 413, 430, 439, 525; 568);

n = 8: (90, 223, 478, 524, 748, 1088, 1190, 1324; 1409)…

Помимо квадратной степени, наименьшими числами отличаются третья и пятая степени. Как главные признаки и определяющие символы трехмерно-материального мира и пятого порядка осевой симметрии живых систем. Причем, 72 = 6·12.

С египетским треугольником всё ясно. Зато остается открытой геометрическая проблема: существует ли треугольник с целочисленными сторонами, медианами и площадью? – Достойная тема для истинного патриота <мета>геометрии.

Плюс бонус: международный престиж страны и благодарная память потомков.

Парадоксы на ровном месте. В учебном пособии [25], направленном на новые знания геометрических начал гармоничного устройства мира и его числовых констант, писатель рассматривает золотое деление отрезка 1 на меньшую x и большую часть 1–x согласно пропорции 1/(1–x) = (1–x)/x, которая неожиданно преобразуется [25, с. 10] в уравнение x² + x – 1 = 0 с решениями (Ф, –ф), и делается вывод о парадоксальном результате: часть больше целого. Писатель подвергает сомнению данный подход, подчеркивая, что только он указал на некорректное алгебраическое вычисление константы, и так далее…

В действительности, пропорция элементарно приводиться к правильному уравнению x² – 3x + 1 = 0 с корнями (ф², Ф²), и нет никакого парадокса. Причем число Ф² ≈ 2,168 выходит за пределы единичного отрезка и означает его деление внешним образом.

«Избавь нас от лукавых» учебников.

Под прикрытием… В кругах водителей известен маневр-поворот автомобиля «под прикрытием». Писатель решил напомнить (АТ, 29.01.2021) о решенных "фундаментальных задачах" (мета-Δ, сакрального тетраэдра, пятиугольной пирамиды с 12 ребрами, полупустого додекаэдра и др.) под прикрытием пропагандируемых идей А.Субетто. Чего стоят только его цитаты без правил русской орфографии:

«Теория Ноосферной (и Космической) Гармонии как Закона бытия Целого в виде Ноосферы входит в Ноосферизм...»;

«Эпоха Великого Эволюционного Перелома в соответствии с вышедший на "арену истории" Большой Логикой Социоприродной Эволюции...»;

«2020 год – год фактической смерти Старой Системы. Отныне Мир должен принять Новый Путь...» и т.д. и т.п.

Такими цитатами детей пугать... А пишут их для большей убедительности, когда не хватает должной аргументации. Прежде всего, убеждая самих себя, налево и направо разбрасываясь прописными буквами, густо удобряя курсивом и жирным шрифтом.

По замыслу идеологов, ноосферизм соединяет учения о социализме, коммунизме и ноосфере. Как «Ноосферный Экологический Духовный Социализм, переходящий в Ноосферный Коммунизм». Или проще – ноосферный неокоммунизм, как нео-"Коммунистическая Сфера Разума" и «проявление рефлексивно-системно-спиральной фило-онтогенетической симметрии и гармонии Мира» (АТ, 22.08.2014).

Но в какие белые одежды не ряди, ноосферно-неокоммунистическая мировоззрение по-прежнему предстает <научной> утопией всеобщего благоденствия, с красивой сказкой о «молочных реках и кисельных берегах» в недостижимой точке "омега".

Само понятие "ноосфера", вокруг которого сегодня столько наукообразия, введено в обиход священником-иезуитом Т.Шарденом и практически повсеместно несет отпечатки религии, подмешанной мистикой и оккультизмом. С негативным отношением и нетерпимостью к общечеловеческим духовно-нравственным и национально-культурным ценностям. Но об этом отдельный разговор....

Только ума не приложу, каким боком "мета-геометрия" соединяется с ноосферным неокоммунизмом. Сдается, через сюрреализм и абстракционизм.

Уловки и приемы эристики. Писательский контатекст высокопарных утверждений на фоне явного преувеличения результатов поражает. Причем с множеством ошибок, противоречий и математического нигилизма, доходящего до откровенного вздора.

Спорить-дискутировать с писателем практически бесполезно. Для него "мета-геометрия" – это сюрреализм, как соединение не соединяемого и сочетание не сочетаемого, по примеру художников М.Эшера, Э.Штейнберга и др. Одновременно "мета-геометрия" – метабазис, как софистский способ, связанный с подменой понятий, отклонением от обсуждаемых вопросов и уходом от темы. – Знакомые многим уловки и приемы эристики [26].

Дискуссия (лат. discussio исследование, рассмотрение, разбор) переводится в русло полемики, цель которой любой ценой защитить, отстоять свое мнение. С навешиванием ярлыков (инсинуаций), как дешевый прием манипуляции и паразитирования на эмоциях. – Любимая технология софистики. С её сужением сути-предмета обсуждения, подменой тезисов, переходом "на личности", обвинениями, запутыванием, взыванием к совести и т.п. Обычные извороты и наскоки на оппонентов.

Плюс ноу-хау: "мета-геометрия" искусно камуфлируется под название "Русский проект", а любой её критик автоматически становится русофобом. Доказательство утверждения, что мета-Δ является частной реализацией Δ-Кеплера, объявляется рейдерским захватом геометрической территории, помеченной писателем, и так далее.

Софисты сознательно опорочивают истину, обеляют ложь. Де-факто демонстрируют полное или частичное отсутствие здравого смысла. Витая в облаках фантасмагории и сюрреальности, предлагая абсурдные и противоречивые сочетания натуралистических образов, совмещая картинки сновидений и реальности.

Плюс гипертрофированное чувство собственной значимости: всё у них эврика, впервые, фундаментально, гениально.

Софистику понимали, хорошо знали и применяли ещё в Древней Греции.

С тех пор много воды утекло. Но в своем природном круговороте она «возвращается сквозь непогоду» (В.Высоцкий).

Всё течёт, но не всё изменяется...

Литература:

1. Хайдеггер М. Что такое метафизика? Пер. с нем. – 2-е изд. – М.: Академический Проект, 2013. – 288 с.
2. Успенский П.Д. Tertium organum. Ключ к загадкам мира. 2-е изд., испр. и доп. – Пг.: Н.П. Таберио, 1916. – 322 с.
3. Холл М. Жизнь и философия Пифагора // Энциклопедическое изложение масонской, герметической, каббалистической и розенкрейцеровской символической философии. Пер. с англ. – Новосибирск: Наука, 1997. – 794 с.
4. Вейль Г. Симметрия. Пер. с англ. – М.: Наука, 1968. – 192 с. – URL: ilib.mirror1.mccme.ru/djvu/weyl-symmetry.htm.
5. Johnson N.W. Convex Polyhedra with Regular Faces // Canad. J. Math., 1966. 18, 169-200.
6. Залгаллер В.А. Выпуклые многогранники с правильными гранями. // Зап. научн. сем. ЛОМИ, 1967, т.2, 5-221.
7. Рассел Б. История западной философии. Космогония Платона. Пер. с англ. – СПб.:: Азбука, 2001. – 956 с. – URL: psylib.org.ua/books/rassb01/.
8. Арнольд В.И., Крылов А.Л. Равномерное распределение точек на сфере и некоторые эргодические свойства решений линейных обыкновенных дифференциальных уравнений в комплексной области // Докл. АН СССР. – 1963. – Т. 148, № 1. – С. 9-12.
9. Василенко С.Л. Золотые купола в задаче конусной упаковки евклидового пространства // Научно-техническая б-ка SciTecLibrary. – 17.07.2011. – URL: sciteclibrary.ru/rus/catalog/pages/11225.html // АТ. – М.: Эл. № 77-6567, публ. 17147, 26.12.2011. – URL: trinitas.ru/rus/doc/0232/013a/02322102.htm.
10. Щетников А.И. Золотое сечение, квадратные корни и пропорции пирамид в Гизе // Историко-математические исследования. – 2009. – № 13(48). – С. 198-217. – URL: nsu.ru/classics/pythagoras/Pyramis.pdf.
11. Василенко С.Л. Треугольник Кеплера как объединитель теоремы Пифагора, золотого сечения и современных мифов // АТ. – М.: Эл. № 77-6567, публ.22385, 05.08.2016. – URL: trinitas.ru/rus/doc/0016/001e/00163016.htm.
12. Василенко С.Л. Золотой прямоугольник Кеплера: свойства, особенности и проявления // АТ. – М.: Эл. № 77-6567, публ.22410, 18.08.2016. – URL: trinitas.ru/rus/doc/0016/001e/00163027.htm.
13. Livio Mario. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. – New York: Broadway Books, 2002. – 292 p.
14. Herz-Fischler R. The shape of the Great Pyramid. – Wilfrid Laurier University Press, 2000. – 293 p.
15. Ворон А.В. Треугольники Кеплера, Фибоначчи и геометрия платоновых тел. – НИЦ ЛАИ. – 30.05.2018. – URL: https://lah.ru/treugolniki-keplera-fibonachchi-i-geometriya-platonovyh-tel/.
16. Ворон А.В. Платоновы тела как структурированные геометрические объекты // АТ. – М.: Эл. № 77-6567, публ. 26288, 08.04.2020. – URL: trinitas.ru/rus/doc/0016/001h/00164335.htm.
17. Василенко С.Л. Семейство золотых треугольников и параллелограммов // АТ. – М.: Эл. № 77-6567, публ. 26931, 23.01.2021. – URL: trinitas.ru/rus/doc/0016/001h/00164608.htm.
18. The On-Line Encyclopedia of Integer Sequences (OEIS). – URL: http://oeis.org/.
19. Василенко С.Л. В погоне за мега-призраками // АТ. – М.: Эл. № 77-6567, публ.24276, 14.02.2018. – URL: trinitas.ru/rus/doc/0016/001f/00163618.htm.
20. Abraham A.A. Solid Analytic Geometry. – Dover Publications, 2016. – 176 p.
21. Начала Евклида. Книги XI–XV: Пер. с греч. – М. –Л.: ГИТТЛ, 1950. – 332 с.
22. Wells D. The Penguin Dictionary of Curious and Interesting Geometry. – London: Penguin, 1991, 304 р.
23. Luminet J.-P., Weeks J., Riazuelo A., Lehoucq R., Uzan J.-P. Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background // Nature, 2003, 425, 593-595. – URL: arxiv.org/abs/astro-ph/0310253.
24. Василенко С.Л. Золотые двуугольники, египетский треугольник и модель всевидящего ока // АТ. – М.: Эл. № 77-6567, публ.22038, 25.04.2016. – URL: trinitas.ru/rus/000/a0000001.htm.
25. Сергиенко П.Я. Новые знания математики гармоничного мироустройства: учеб. пособие. – М.: Lennex Corp, 2013. – 51 с.
26. Жмудь В.А. О принципиальном отличии методов доказательств от методов убеждений // Автоматика и программная инженерия. – 2013, №3(5), 87-104.

[Обсуждение на форуме «Публицистика»]